Video: ¿Cómo demuestras que las diagonales de un rombo se bisecan entre sí?
2024 Autor: Lynn Donovan | [email protected]. Última modificación: 2023-12-15 23:45
en un rombo todo los lados son iguales y los lados opuestos son paralelos. Además un rombo es también un paralelogramo y, por lo tanto, exhibe propiedades de un paralelogramo y eso las diagonales de un paralelogramo se bisecan entre sí.
En consecuencia, ¿las diagonales de un rombo se bisecan entre sí?
En cualquier rombo , los diagonales (líneas que unen esquinas opuestas) bisectarse el uno al otro en ángulo recto (90 °). Es decir, cada diagonal corta el otro en dos partes iguales, y el ángulo donde se cruzan es siempre de 90 grados. En la figura de arriba, arrastre cualquier vértice para remodelar el rombo y convéncete de que esto es así.
En segundo lugar, ¿las diagonales de los rombos son perpendiculares? Propiedades de un Rombo los diagonales están perpendicular y se bisecan entre sí. Los ángulos adyacentes son suplementarios (por ejemplo, ∠A + ∠B = 180 °). A rombo es un paralelogramo cuyo diagonales están perpendicular el uno al otro.
Teniendo esto en cuenta, ¿cómo se prueba que las diagonales de un rombo son bisectrices perpendiculares?
Prueba que el las diagonales de un rombo son perpendiculares Continuación de lo anterior prueba : Las partes correspondientes de triángulos congruentes son congruentes, por lo que los 4 ángulos (los del medio) son congruentes. Esto lleva al hecho de que todos son iguales a 90 grados, y la diagonales están perpendicular el uno al otro.
¿Es el rombo un paralelogramo?
DEFINICIÓN: A rombo es un paralelogramo con cuatro lados congruentes. TEOREMA: Si un paralelogramo es un rombo , cada diagonal divide en dos un par de ángulos opuestos. TEOREMA Converse: Si un paralelogramo tiene diagonales que bisecan un par de ángulos opuestos, es un rombo.
Recomendado:
¿Las diagonales siempre se bisecan entre sí en un paralelogramo?
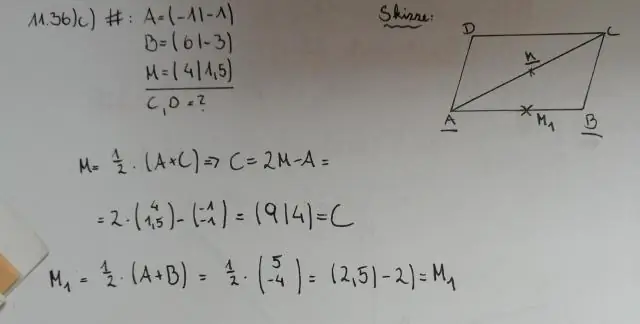
En cualquier paralelogramo, las diagonales (líneas que unen esquinas opuestas) se bisecan entre sí. Es decir, cada diagonal corta a la otra en dos partes iguales. En la figura anterior, arrastre cualquier vértice para remodelar el paralelogramo y convénzase de que esto es así
¿Las diagonales del paralelogramo se bisecan entre sí en 90?
En cualquier rombo, las diagonales (líneas que unen las esquinas opuestas) se bisecan entre sí en ángulos rectos (90 °). Es decir, cada diagonal corta a la otra en dos partes iguales, y el ángulo donde se cruzan es siempre de 90 grados
¿Qué paralelogramos tienen diagonales que se bisecan entre sí?
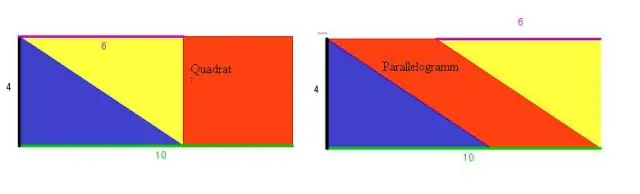
Si dos lados adyacentes de un paralelogramo son iguales, entonces es un rombo. Esta prueba a menudo se toma como la definición de un rombo. Un cuadrilátero cuyas diagonales se bisecan en ángulos rectos es un rombo
¿Cómo demuestras la resolución creativa de problemas?
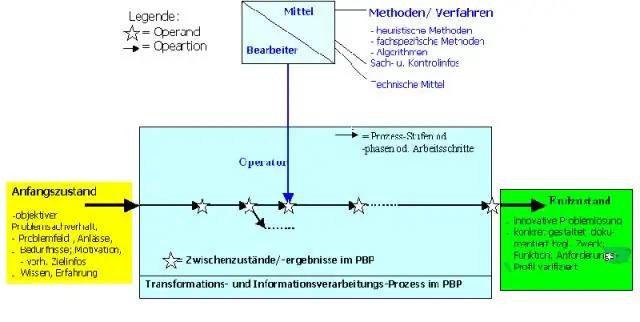
Veamos cada paso más de cerca: Aclare e identifique el problema. Podría decirse que el paso más importante de CPS es identificar su problema o meta real. Investiga el problema. Formule uno o más desafíos creativos. Genera ideas. Combinar y evaluar ideas. Elabora un plan de acción. ¡Hazlo
¿Cómo demuestras una fuerte inducción?
El principio de inducción fuerte dice que puede probar un enunciado de la forma: P (n) para cada entero positivo n. como sigue: Caso base: P (1) es verdadero. Paso inductivo fuerte: Suponga que k es un número entero positivo tal que P (1), P (2), P (k) son todos verdaderos. Demuestre que P (k + 1) es cierto