Video: ¿Qué es la búsqueda primero en amplitud y la búsqueda en profundidad primero?
2024 Autor: Lynn Donovan | [email protected]. Última modificación: 2023-12-15 23:45
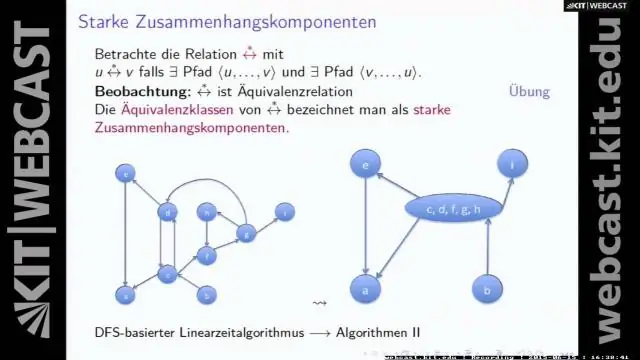
BFS representa Primera búsqueda de amplitud . DFS representa Primera búsqueda en profundidad . 2. BFS ( Primera búsqueda de amplitud ) utiliza la estructura de datos de la cola para encontrar la ruta más corta. BFS puede ser usado encontrar la ruta más corta de una sola fuente en un gráfico no ponderado, porque en BFS , llegamos a un vértice con un número mínimo de aristas desde un vértice de origen.
Por lo tanto, ¿qué es la búsqueda en profundidad primero con ejemplo?
Primera búsqueda en profundidad o DFS para un gráfico. Profundidad primer recorrido (o Buscar ) para un gráfico es similar a Profundidad primer recorrido de un árbol. Para ejemplo , en el siguiente gráfico, comenzamos el recorrido desde el vértice 2. Cuando llegamos al vértice 0, Mira para todos los vértices adyacentes de la misma. 2 también es un vértice adyacente de 0.
Además de arriba, ¿qué devuelve la búsqueda en profundidad? los profundidad - primera busqueda El algoritmo nos permite determinar si dos nodos, el nodo x y el nodo y, tienen una ruta entre ellos. El algoritmo DFS lo hace esto mirando a todos los hijos del nodo inicial, nodo x, hasta que alcanza el nodo y.
Del mismo modo, ¿qué es la búsqueda primero en amplitud?
Primera búsqueda de amplitud (BFS) Algoritmo Amplitud primera búsqueda es un grafico el recorrido algoritmo que comienza a atravesar el gráfico desde el nodo raíz y explora todos los nodos vecinos. Luego, selecciona el nodo más cercano y explora todos los nodos inexplorados.
¿De qué sirve la búsqueda en profundidad?
Profundidad - primera busqueda se utiliza en clasificación topológica, problemas de programación, detección de ciclos en gráficos y resolución de acertijos con una sola solución, como un laberinto o un sudoku. Otras aplicaciones implican analizar redes, por ejemplo, probar si un gráfico es bipartito.
Recomendado:
¿Es la búsqueda lineal lo mismo que la búsqueda secuencial?
Clase: algoritmo de búsqueda
¿Qué profundidad tienen los accesorios SharkBite?
Conexiones SharkBite / Compatibilidad de tamaño de tubería / Profundidad de inserción de tubería Tamaño de conexión SharkBite (pulg.) Tamaño nominal de tubería Profundidad de inserción de tubería Fracción (pulg.) 3/8 3/8 pulg. CTS 1 1/2 1/2 pulg. CTS 1 5 / 8 5/8 pulg. CTS 1-1 / 8 3/4 3/4 pulg. CTS 1-1 / 8
¿Qué profundidad tiene el orificio de un poste de buzón?
Use una excavadora de agujeros para postes para cavar un agujero para su poste en este lugar. Excave lo suficientemente profundo como para que la altura de su buzón sobre el suelo sea de alrededor de 42 pulgadas. No excave más de 24 pulgadas
¿Qué son los motores de búsqueda que buscan en otros motores de búsqueda?
Para comenzar nuestra aventura de búsqueda, veamos algunos motores de búsqueda generales más allá de los tres primeros. Pato Pato a ganar. ¿Le preocupa la privacidad en línea? Search Encrypt. ¿Está buscando una alternativa a DuckDuckGo? Ecosia. ¿Quieres plantar árboles mientras buscas? Dogpile. Blekko. Wolfram Alpha. Gigablast. Búsqueda de Facebook
¿Qué es la búsqueda de amplitud primero en inteligencia artificial?
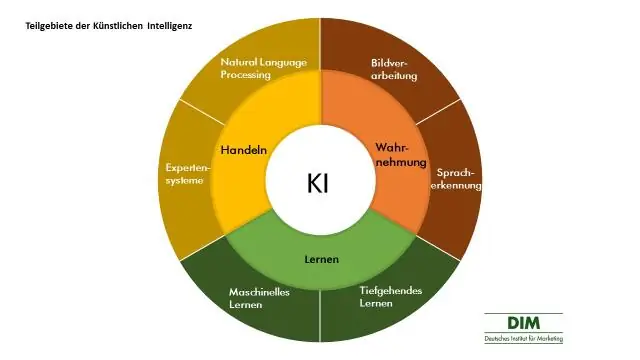
Publicado el 4 de abril de 2017. La búsqueda en amplitud es como atravesar un árbol en el que cada nodo es un estado que puede ser un candidato potencial para la solución. Expande los nodos desde la raíz del árbol y luego genera un nivel del árbol a la vez hasta que se encuentra una solución