
- Autor Lynn Donovan [email protected].
- Public 2023-12-15 23:45.
- Última modificación 2025-01-22 17:22.
Regularización . Esta es una forma de regresión , que restringe / regulariza o reduce las estimaciones de coeficientes hacia cero. En otras palabras, esta técnica desalienta el aprendizaje de una forma más compleja o flexible. modelo , para evitar el riesgo de sobreajuste. Una simple relación para regresión lineal Se ve como esto.
En consecuencia, ¿qué es lambda en regresión lineal?
Cuando tenemos un alto grado lineal polinomio que se utiliza para ajustar un conjunto de puntos en un regresión lineal configuración, para evitar el sobreajuste, utilizamos la regularización e incluimos un lambda parámetro en la función de costo. Esta lambda luego se usa para actualizar los parámetros theta en el algoritmo de descenso de gradiente.
En segundo lugar, ¿cuál es el propósito de la regularización? Regularización es una técnica utilizada para ajustar el función agregando un término de penalización adicional en el error función . El término adicional controla la fluctuación excesiva función de manera que los coeficientes no tomen valores extremos.
De esta forma, ¿por qué necesitamos regularizar en regresión?
El objetivo de regularización es evitar el sobreajuste, es decir nosotros están tratando de evitar modelos que se ajustan extremadamente bien a los datos de entrenamiento (datos usados para construir el modelo), pero que se ajustan mal a los datos de prueba (datos usados para probar qué tan bueno es el modelo). Esto se conoce como sobreajuste.
¿Qué significa regularización?
En matemáticas, estadística e informática, particularmente en aprendizaje automático y problemas inversos, la regularización es el proceso de agregar información para resolver un problema mal planteado o para evitar un sobreajuste. Regularización se aplica a funciones objetivas en problemas de optimización mal planteados.
Recomendado:
¿Qué es lineal y no lineal en la estructura de datos?

1. En una estructura de datos lineal, los elementos de datos se organizan en un orden lineal donde todos y cada uno de los elementos se adjuntan a su anterior y siguiente adyacente. En una estructura de datos no lineal, los elementos de datos se adjuntan de manera jerárquica. En la estructura de datos lineal, los elementos de datos se pueden atravesar en una sola ejecución
¿Qué es la regresión ML?
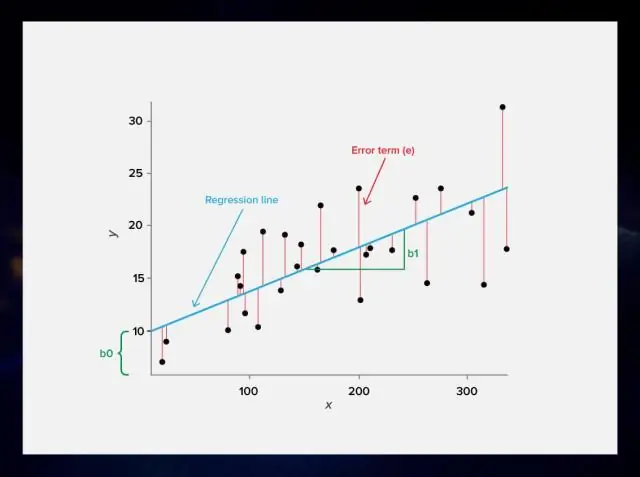
La regresión es un algoritmo ML que se puede entrenar para predecir salidas numeradas reales; como temperatura, precio de las acciones, etc. La regresión se basa en una hipótesis que puede ser lineal, cuadrática, polinomial, no lineal, etc. La hipótesis es una función que se basa en algunos parámetros ocultos y los valores de entrada
¿Qué es el método del árbol de regresión?

La metodología de construcción del árbol de regresión general permite que las variables de entrada sean una mezcla de variables continuas y categóricas. Un árbol de regresión puede considerarse como una variante de los árboles de decisión, diseñado para aproximar funciones de valor real, en lugar de utilizarse para métodos de clasificación
¿Qué es un problema de regresión en el aprendizaje automático?
Un problema de regresión es cuando la variable de salida es un valor real o continuo, como "salario" o "peso". Se pueden utilizar muchos modelos diferentes, el más simple es la regresión lineal. Intenta ajustar los datos con el mejor hiperplano que pasa por los puntos
¿Qué es el análisis de árbol de regresión?

El análisis del árbol de regresión es cuando el resultado predicho puede considerarse un número real (por ejemplo, el precio de una casa o la duración de la estadía de un paciente en un hospital)
