Video: ¿Cuál es la diferencia entre un diagrama de caja y bigotes y un diagrama de caja?
2024 Autor: Lynn Donovan | [email protected]. Última modificación: 2023-12-15 23:45
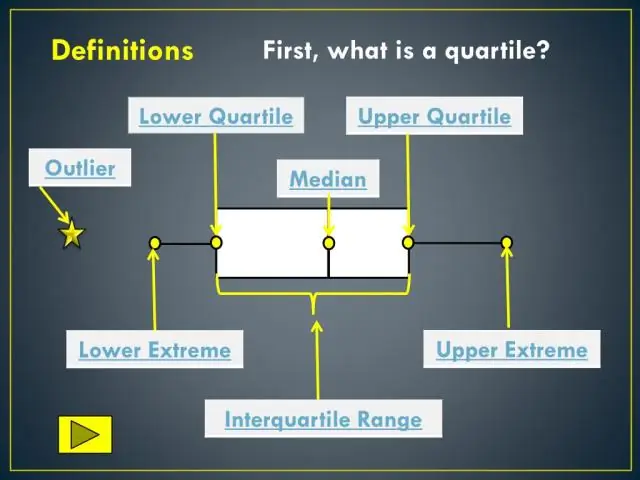
A diagrama de caja y bigotes (a veces llamado diagrama de caja ) es un grafico que presenta información de un resumen de cinco números. En un diagrama de caja y bigotes : los extremos de la caja son los cuartiles superior e inferior, por lo que caja abarca el rango intercuartílico. la mediana está marcada por una línea vertical dentro del caja.
Con respecto a esto, ¿qué significa el diagrama de caja y bigotes?
A diagrama de caja y bigotes se define como un método gráfico para mostrar la variación en un conjunto de datos. En la mayoría de los casos, un análisis de histograma proporciona una visualización suficiente, pero diagrama de caja y bigotes puede proporcionar detalles adicionales al tiempo que permite que se muestren varios conjuntos de datos en el mismo gráfico.
Además, ¿cómo se calcula un diagrama de caja? Para crear un caja -y-bigotes trama , comenzamos ordenando nuestros datos (es decir, poniendo los valores) en orden numérico, si aún no están ordenados. Luego encontramos la mediana de nuestros datos. La mediana divide los datos en dos mitades. Para dividir los datos en cuartos, luego encontramos las medianas de estas dos mitades.
También sepa, ¿qué nos dicen los diagramas de caja?
A diagrama de caja es una forma estandarizada de mostrar la distribución de datos basada en un resumen de cinco números (“mínimo”, primer cuartil (Q1), mediana, tercer cuartil (Q3) y “máximo”). Eso Puedo decir sobre sus valores atípicos y cuáles son sus valores.
¿Cómo se determinan los valores atípicos?
Un punto que cae fuera de los límites internos del conjunto de datos se clasifica como menor. parte aislada , mientras que uno que cae fuera de las vallas exteriores se clasifica como un importante parte aislada . Para encontrar las cercas internas para su conjunto de datos, primero, multiplique el rango intercuartil por 1.5. Luego, sume el resultado a Q3 y réstelo de Q1.
Recomendado:
¿La unidad está probando una caja blanca o una caja negra?
Es decir, la prueba unitaria se refiere al nivel en el que tiene lugar la prueba en la estructura del sistema, mientras que las pruebas de caja blanca y negra se refieren a si, en cualquier nivel, el enfoque de la prueba se basa en el diseño interno o solo en la especificación externa de la unidad
¿Qué son las pruebas de caja negra y caja blanca?
Black Box Testing es un método de prueba de software en el que el evaluador no conoce la estructura, el diseño o la implementación internos del elemento que se está probando. White Box Testing es un método de prueba de software en el que el probador conoce la estructura / diseño / implementación internos del elemento que se está probando
¿Qué es un diagrama de caja agrupado?
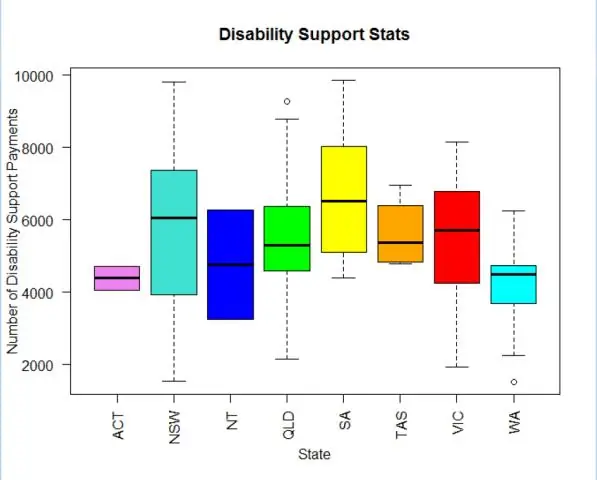
La gráfica de caja agrupada puede mostrar gráficas de caja para cada combinación de los niveles de dos variables independientes. Se revisan los elementos del diagrama de caja y cómo detectar valores atípicos utilizando el rango intercuartílico (IQR)
¿Cuál es la diferencia entre la compresión entre cuadros e intracuadros?
La compresión intracuadro solo ocurre dentro de cada cuadro. La compresión entre cuadros utiliza este hecho para comprimir imágenes en movimiento. La compresión entre cuadros implica el análisis de los cambios en la película de un cuadro a otro y toma nota solo de las partes de la imagen que han cambiado
¿Cuál es la similitud y cuál es la diferencia entre relés y PLC?
Los relés son interruptores electromecánicos que tienen bobina y dos tipos de contactos NO y NC. Pero un controlador lógico programable, PLC es una mini computadora que puede tomar decisiones en función del programa y su entrada y salida